Brain Teasers ? or 50 Years On........... ?

A semi-circular lorry park could be created with c.25% more area  (ratio = 4/&Pi, but as you say, that might not be so efficient for parking.

That should read "Ratio equals four divided by Pi"

I had thought that by selecting "Insert Special Character" ( the omega sign on the Tool Bar) Hopeless would have inserted the standard "Pi" sign. So much for hoping where Hopeless is concered !

I seem to have missed the submit an answer to the last one, so I'll pile in on this one and say that the scales will go down on the left. The right-hand ball, no matter what it's filled with and even no matter how big it is won't have the slightest effect on the scales, as long as it doesn't touch the sides.

If I might pile in on the questioning front as well, here's one from me:

A lit candle is stood securely in an open jam jar, burning quite happily. It is suspended from a support by a piece of string. The string is then suddenly and cleanly cut and the jar and candle fall vertically downwards. As this happens, what happens to the candle flame?

Mark

More than 12 years ago !! Those 288 balls kept us all working for weeks !!

That's the least of your worries, there's no gate! 

Oh bother ! I just knew there was something missing.....

Well, the situation is finely balanced (apologies for the pun)

Left down : Mulberry, Willy, Ebor

Level : Chris SU

Right down : Fat Cat, Winky, Lionel

The right side down team have it !

Winy and FatCat's explanations are as good as (or better than) mine and

Lionel's experiment kinda clinches it....

But please challenge winky, fatcat, Lionel and myself if you need further explanation.

hmmm, nice one -lets give it a starter for ten...........

If the candle is short in relation to the height of the jam jar, then i'm inclined to think that :-

• air movement into/out-of the jar will be minimal
• gravity will cease to exist in respect of the flame so it will become spherical
• convection of the flame gasses will reduce
• inward flow of new air/oxygen towards the flame will reduce
• the flame will dim, or possibly go out

If the candle is almost as tall as the jam jar then airflow around the top of the jar and the flame could be complex and I think Lionel should perform an experiment

In fact, I think Lionel might perform an experiment anyway - the Forum's answer to the re-energised Large Haldron Collider

You willing to give it a go Lionel ?

I'd say the flame would elongate into a cylinder the same diameter as the candle, with a pointy tip.

Because the candle is dropping, the flame won't have time assume the teardrop shape. I don't think the flame will go out, the flame gasses will still be be produced in the same quantity, but change shape.

Or, maybe not.

Originally Posted by Ebor:

I seem to have missed the submit an answer to the last one, so I'll pile in on this one and say that the scales will go down on the left. The right-hand ball, no matter what it's filled with and even no matter how big it is won't have the slightest effect on the scales, as long as it doesn't touch the sides.

 

If I might pile in on the questioning front as well, here's one from me:

 

A lit candle is stood securely in an open jam jar, burning quite happily. It is suspended from a support by a piece of string. The string is then suddenly and cleanly cut and the jar and candle fall vertically downwards. As this happens, what happens to the candle flame?

 

Mark

could be complex and I think Lionel should perform an experiment

 

You willing to give it a go Lionel ?

Alas, I doubt I  have a ladder tall enough...

Also, the question needs more detail, I  think. As you say. how high is the candle in relation to the jar; from what height is the jar dropped; is air pressure constant throughout the drop? I agree with Don that during the drop the situation would be as he describes. If the flame could survive until  terminal velocity was reached, then convection would operate again and the flame would assume a more natural profile.

In a sealed system - the International Space Station for example where everything is falling at the same constant  rate, I would agree with Don that the flame would be spherical and, becasue of the "absence" of gravity there would be no convection and the flame would die for want of oxygen.

Yeah, I think you've all got that one. The free-fall of the candle effectively 'switches off' gravitational effects on the flame, exactly as happens in stable orbiting spacecraft, as Lionel pointed out. Convection effects disappear in the absence of gravity, so the flame would become temporarily spherical before going out due to lack of oxygen. NASA has done experiments on flames in microgravity environments - it's worth a google if you're interested.

This next one requires a little more background knowledge, but we seem to have a fair amount of that on the forum, so here goes:

If you watch the bubbles rising in a liquid (lemonade, champagne etc.) you will notice them being produced at a fairly constant rate and streaming upwards. As they move upwards, they spread out which shows they are accelerating.

Now, you may think that's totally logical, since the bubbles experience less pressure from the surrounding liquid as they rise, therefore the bubbles expand, displace more water, experience more upthrust and that's why they accelerate.

"Ah but" you might then think, as the bubbles expand, "wouldn't they also experience more drag and so not accelerate after all? But I can see them accelerating, so there must be some reason why the extra drag doesn't cancel out the extra upthrust". What might that reason be?

Mark

That example looks very similar to me, to a stationary sphere in a moving flow. The size of a stationary sphere has no effect on drag if the flow has a very low Reynolds number. Reynolds number is proportional to speed of flow, could it be the bubbles are travelling so slowly, their size has no effect on drag.

Having recently looked at a carbonated beverage, I am not sure that bubbles actually accelerate as they rise. Certainly they expand, but do they accelerate?

Can you prove that they accelerate?

This is the sort of thing I've seen happening consistently in the fizz I've drunk over the years (observed before I've drunk too much, before you ask):

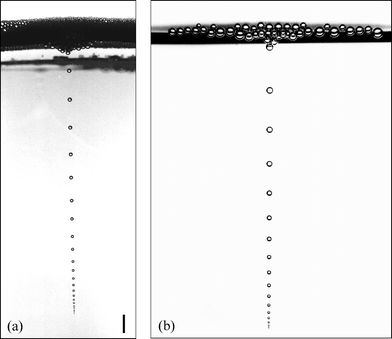
As long as the bubbles are being produced at a constant rate (and they definitely seem to be to my eyes), the fact that their spacing increases as they rise shows they must be accelerating.

Mark

Having thought about it a bit more, it must be true that as bubbles rise pressure must decrease and the volume of the bubble will increase.

I have just found this: news.stanford.edu/news/2001/november7/beer-117.html which might explain it...

I think the link I posted says as much?

Is that a question!

Ho Ho Ho !!!

I think it was. But not so remarkable  a question as to attract such an exclamated statement about it ! 

I also noticed that Lionel's link asserts that air bubbles in water do not accelerate as they rise. I does explain why CO2 bubbles in carbonated liquids  expand and accelerate.

Mark's post does specifically mention bubbles in fizz, lemonade and champagne, so observations based on air bubbles in water would be misleading.

Nice link Lionel. And a nice summary Chris.

I did suggest a semi-circle and it clearly increases the enclose area compared to a rectangle.

Since a rectangle (ratio 2:1) encloses a larger area than a square, I did wonder if a semi-ellipse might generate a larger area than a semicircle.

The area of an ellipse is given by Pi*a*b where a and b are the major and minor radii.

The circumference of an ellipse is.........................life's too short !!

The exclamation mark is often described in the print media as a "screamer". It also often describes those who use it...

Crikey, I think my original question might have been misinterpreted. Let me rephrase it in a slightly more formal way:

A bubble forms at a nucleation point in a glass, grows to a sufficient size to detach itself from the glass and rises through the liquid in the glass. As it rises it grows in volume and accelerates. The growth in volume causes an increase in drag force but also an increase in the upthrust the bubble experiences. The bubble's acceleration shows that the increase in upthrust is not cancelled out by the increase in drag force. Why not?

Mark

The force upwards is loosely a function of the volume, whereas the drag is loosely a function of surface and/or cross-sectional area. As a bubble grows, both dimensions grow, but volume is proportional to radius cubed whereas area is proportional to radius squared. So as the bubble grows, the upwards force grows more quickly than the drag does, meaning an increase in speed is required to stay at equilibrium.

Ebor

My post a few posts above has a link to propagation of bubbles in carbonated beverages. I hesitate to indicate a rhetorical question with a question mark lest Adam duck tries to go mediaeval on my arse...