A Fistful of Brain Teasers

Don Atkinson posted:

Now, as far as I know, this one has only one solution. ( I can't guarantee that, but I do believe it is the case)  And I hope (and pray) that I haven't muddled up the wording to confuse Steve (or anybody else) or allow IB to spot an ellipsis....

Animal Farm (fingers crossed)

A farmer went to market and bought a hundred animals at a total cost of £100. He bought a mixture of cows, sheep and chickens. The price of cows was £5 each, Sheep £1 each and chickens £1  1 shilling each.

How many of each kind did he buy, ?

I have modified the text to :-

a) correct an error about the price of chickens (real apologies)

b) make it clear that he bought a mixture each and every animal (avoid too much ambiguity, otherwise he could have bought 100 sheep)

c) however, there might be a perceived ellipsis, surrounding the word "sheep". Although I never noticed this when I first encountered this teaser, I have become sensitive to this sort of thing this past week !!!! ("sheep" can be both singular and plural)

Despite almost having to provide the answer in order to clarify the wording, you might still find it an interesting challenge.

Innocent Bystander posted:

And I'm guessing the question is missing some info about the types of animal the farmer actually buys (including not omitting any animal type)?

That is a clearer way of wording what he bought, without making the solution too obvious. Thank you IB.

I rather fear that this particular "teaser" is now more about me getting the wording right rather than others getting an answer !!

Don

I get 19 cows, a lone sheep and 80 chickens ?

Regards,

Peter

sophiebear0_0 posted:

Don

I get 19 cows, a lone sheep and 80 chickens ?

Regards,

Peter

That’s spot-on Peter..

Thank goodness I eventually got the wording more or less right.

I rather suspect that both Steve and IB had figured out the answer as well, despite my dreadful presentation. Qudos to them too.

Thanks to all for persevering!

Now, back to those 288 balls.....

sophiebear0_0 posted:

Don

I get 19 cows, a lone sheep and 80 chickens ?

Regards,

Peter

Did you use the "brute force" technique ? or did you generate a couple of simultaneous equations to reduce the guess work ? I appreciate it's not possible to generate three equations, but generating two usually helps.

Don

I did use a couple of simultaneous equations (combined with the logic that cows needed to be integer !). So it went along the lines:

1) X + Y + Z =100

2) 5X + Y +0.05 Z =100

where X=cows; Y=sheep & Z= chickens.

As you say, you can't solve for 3 unknowns with 2 equations - but  you can subtract 1) from )2 to get X in terms of Z. Then you need to see what solutions will give you whole chickens and whole cows.

Regards,

Peter

Innocent Bystander posted:

Indeed (and I only want to be told the solution in order to be able to check and (maybe!) prove wrong! I,ll have another look later this eve or tomorrow ...unless someone beats me to it

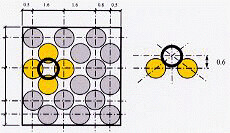
Got there at last! 2 gross of balls (288). I tried 4,3,4,3,4, to no avail. Led me to 3,3,3,3,3,3. I then had to work out spacing, one end row ball up agains a side wall, which took me some rough drawing, three equations to solve and one single pythagorus calc. And it all fits - perfectly! Spacing 0.6cm between balls in horizontal rows, in both directions parallell to the box sides (box with 5cm square at bottom). Alternate vertical layers identical but 'flipped', spacing between layer centres also 0.6cm. No possible movement of anything once the box is packed and lidded. Very neat! (But may be challenging to pack!)

Innocent Bystander posted:

Innocent Bystander posted:

Indeed (and I only want to be told the solution in order to be able to check and (maybe!) prove wrong! I,ll have another look later this eve or tomorrow ...unless someone beats me to it

Got there at last! 2 gross of balls (288). I tried 4,3,4,3,4, to no avail. Led me to 3,3,3,3,3,3. I then had to work out spacing, one end row ball up agains a side wall, which took me some rough drawing, three equations to solve and one single pythagorus calc. And it all fits - perfectly! Spacing 0.6cm between balls in horizontal rows, in both directions parallell to the box sides (box with 5cm square at bottom). Alternate vertical layers identical but 'flipped', spacing between layer centres also 0.6cm. No possible movement of anything once the box is packed and lidded. Very neat! (But may be challenging to pack!)

Satisfaction guaranteed !! it all works out so neatly hey !

Well done IB.

The way I describe it is each layer comprises 18 balls arranged in two, interlaced 3x3 grids. Alternate layers "flipped" as you say.

I'll see if I can post a picture.

Cheers, Don

Not my best picture, but it illustrates the layout of each layer (18 balls), the spacing of the balls including the vertical interval of each layer.

btw,

a little thought will reveal that the spacing of the balls, including the 0.6cm "altitude" involves nothing more than a 3/4/5 triangle.

The slope is 1.0        (ball diameter)

the base is 0.8         (1.6 ÷ 2)

the height is therefore 0.6  (based on pythag using 5/4/3 or actually working out !)

Indeed a single pythag calc was the case for the vertical spacing  (though I didn't spot it as a 3,4,5 triangle in the process).  But it was the horizontal spacing that took a bit of sorting - one row of 3. First ball touching one end, 2cm total space, but approtioned how? Imhad to picture the beginning of a 4th ball at the boundary, and draw a few lines and assign some variables to solve. Maybe there's some simpler explanation I should have seen... but it was simple when once I set it out on paper.

Innocent Bystander posted:

Indeed a single pythag calc was the case for the vertical spacing  (though I didn't spot it as a 3,4,5 triangle in the process).  But it was the horizontal spacing that took a bit of sorting - one row of 3. First ball touching one end, 2cm total space, but approtioned how? Imhad to picture the beginning of a 4th ball at the boundary, and draw a few lines and assign some variables to solve. Maybe there's some simpler explanation I should have seen... but it was simple when once I set it out on paper.

Based on symmetry, the alternating rows of three balls are spaced 0.5/0.8/0.8/0.8/0.8/0.8/0.5 in both directions.

Allowing for the end balls, (5cm minus 2x0.5cm) gives 4cm for the spacing, which divided by five gives the 0.8cm grid in the picture I posted.

I would agree that it's much easier to analyse once the problem has been solved. And it's very satisfying solution.

I would now like to give credit and thank Matthew T for the spheres-in-the-box puzzle. Thank you Matthew.

After the trials and tribulations of the 288 balls, I think a nice, easy relaxing walk with the dog is in order....

One Man and his Dog..

One morning Alex set off at 9 o’clock from his hotel in Bristol and had been walking for an hour at a steady 2 mph when Brian set off after him walking along the same road at a steady 4 mph.

Brian’s dog, Charlie, started at the same time as his master Brian and ran uniformly  forwards and backwards between him and Alex at 10 mph until Brian caught up with Alex.

How far had Charlie run when Brian caught up with Alex ?

Neglect the length of the dog and the time spent in turning.

One man and his dog:-

I calculate that Charlie will have run 10 miles

Does anybody other than me consider Steve to be right ?

Yes. In 1 hr Alex will have walked a further 2 miles, 4 total and Brian will have walked that 4, so caught up at 1 hr, Charlie active for that 1 hrat 10mph = 10 miles. It might have been interesting to consider Charlie's actual movements, but that's a other matter...

Yes the beauty of this puzzle is to ignore the dog's movements and instead focus on Brian's catch-up time. 

Well done Steve, you are right, It's the length of time, not the to&fro movements that really matter.

Clearly IB had similar thinking as well and nicely elaborated for the benefit of browsers.

Famous Five ?

Five Forum Members were playing a game of cards .

A set of cards numbered 1 to 10 (inclusive) was dealt so that each member received two cards.

Mark had two cards which totalled 11, Mike had two cards which totalled 7, Debs had two cards which totalled 17, Mick had two cards which totalled 4 and Eloise had two cards which totalled 16.

In this game the winner is the person who holds the  card numbered 10. Who won the game ?

PS enjoy these easy ones whilst they last.............

.......the next hard one is.......well, you don't want to know !

Eloise. Too easy - a member who always has top arguments!

Another easy one about a coach load of people on a cheap-skate outing....

A coach load of people on an outing went into a café for a snack. The party leader ordered a cup of tea and a sandwich for each person in the party, (including himself and the driver). The total bill came to £18.49. How many people were in the coach party (including the leader and the driver)?

OK no discounts, no special offers, just whole pennies or pounds or whatever !!

Don Atkinson posted:

Another easy one about a coach load of people on a cheap-skate outing....

A coach load of people on an outing went into a café for a snack. The party leader ordered a cup of tea and a sandwich for each person in the party, (including himself and the driver). The total bill came to £18.49. How many people were in the coach party (including the leader and the driver)?

OK no discounts, no special offers, just whole pennies or pounds or whatever !!

Presumably this is remembered from several decades below, maybe 1970s as it was post decimalisation, though I don’t remember whether a drink and sandwich was this cheap even then!

Don Atkinson posted:

Another easy one about a coach load of people on a cheap-skate outing....

A coach load of people on an outing went into a café for a snack. The party leader ordered a cup of tea and a sandwich for each person in the party, (including himself and the driver). The total bill came to £18.49. How many people were in the coach party (including the leader and the driver)?

OK no discounts, no special offers, just whole pennies or pounds or whatever !!

Unless I’ve misdivided by a prime somewhere, 43 people in total.