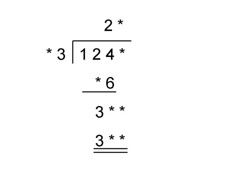A Fistful of Brain Teasers
Posted by: Don Atkinson on 13 November 2017
A Fistful of Brain Teasers
For those who are either non-British, or under the age of 65………. The UK used to have a brilliant system of currency referred to as “Pounds, Shillings and Pence”. Simplified to £ ״ s ״ d. No! Don’t ask me why the “Pence” symbol is a “d”, just learn it and remember it !
A £ comprised 20 Shillings and a Shilling comprised 12 Pence. Thus a £ comprised 240 Pence. I reckon that both Microsoft and Apple would have difficulty with these numbers in their spreadsheets, more so if we included Guineas, Crowns, Half-Crowns and Florins. However, I digress..............
The purpose of the explanation is to assist with the first two or three teasers that follow. So just to ensure a reasonable comprehension has been grasped…. ….. if each of three children has £3 − 7s − 9d, then collectively they have £10 − 3s − 3d Got the idea ? Good ! Just try 5 children, two each with £4 − 15s − 8d and three each with £3 − 3s − 4d. How much do they have between them ? (this isn’t the first brain teaser, just the basic introduction with some “homework”, the Teasers follow)
Innocent Bystander posted:Don Atkinson posted:Another easy one about a coach load of people on a cheap-skate outing....
A coach load of people on an outing went into a café for a snack. The party leader ordered a cup of tea and a sandwich for each person in the party, (including himself and the driver). The total bill came to £18.49. How many people were in the coach party (including the leader and the driver)?
OK no discounts, no special offers, just whole pennies or pounds or whatever !!
Presumably this is remembered from several decades below, maybe 1970s as it was post decimalisation, though I don’t remember whether a drink and sandwich was this cheap even then!
The maths book from which it was taken, was first published in 1987 (it was for one of my daughters, not me !)
So I guess the draft was produced c. 1985. But yes, 43p for a cup of tea and a sandwich does seem a bit far-fetched. btw, 1849 is a "square" number = 43 x 43
Eoink posted:Don Atkinson posted:Another easy one about a coach load of people on a cheap-skate outing....
A coach load of people on an outing went into a café for a snack. The party leader ordered a cup of tea and a sandwich for each person in the party, (including himself and the driver). The total bill came to £18.49. How many people were in the coach party (including the leader and the driver)?
OK no discounts, no special offers, just whole pennies or pounds or whatever !!
Unless I’ve misdivided by a prime somewhere, 43 people in total.
no misdivision Eoink ! it's 43 for sure.
When I first encountered some of these puzzles, home PCs were few and far between, so finding the first Prime in 1849 took a bit of effort to do manually. And even with a BBC Model B (it's in the loft but I think that's the model) it would have taken longer to write a programm to search for prime numbers
Today, I just whacked 1849 into Excel and divided by the numbers 1 to 100 in turn to find 43 again. Took less than a minute ! How times have changed hey !
Now for something a little more challenging ![]()
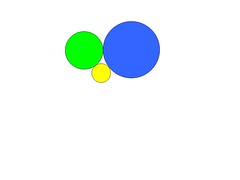
Four Circles
Its (pretty) obvious that the maximum number of different sized circles (excluding infinitely large circles that have become straight lines!) that can be made to 'just touch' one another is four. (each and every circle just touches the other three).
In the attached diagram above, the three circles (Yellow), (Green) and (Blue) have radii of 1, 2 and 3 respectively.
What are the radii of the two 'fourth' circles (shown in red in the diagram below), that can be made to just touch each of Yellow, Green and Blue. (note the two 'fourth' circles will not touch each other, ‘cos that would break the maximum rule!!)
Oh! BTW, there is a standard way and an elegant way to solve this little problem.
Very confused by question.
Yellow r = 1, green r = 2, Blue r = 3
Ah, I think you may have just changed the lower diagram.
So you want the radius of the red circle and what I'm going to call the white circle? Jeez!
Any more editing of this question Don, and there are going to be stiff letters to the Telegraph demanding that the head of the examining board is sacked ![]()
C.
Christopher_M posted:Very confused by question.
Yellow r = 1, green r = 2, Blue r = 3
Ah, I think you may have just changed the lower diagram.
So you want the radius of the red circle and what I'm going to call the white circle? Jeez!
"Yellow r = 1, Green r = 2, Blue r = 3"........this part of the question Chris, you've got absolutely correct - well done !!! ![]()
But IB had complained once too often ![]() that the questions were too easy (easy for some ? perhaps !)
that the questions were too easy (easy for some ? perhaps !)
So on this occasion I added the little solid red circle and the big "empty" red circle, just to make this question a little bit more of a challenge than simply associating "1" with "yellow", "2" with Green etc....![]()
And in doing so, I made a mistake, which I considered I should rectify to avoid confusion ![]()
And yes ! you have correctly identified the required answer(s) ie the radius of the red circle and what you are going to call the white circle? ![]()
I hope this is all crystal clear, ?
Jeez ! the effort I have to put in these days just to please some people.....![]()
enjoy, (as ken c would say !) hopefully.........![]()
I hope the "Head of the Examining Board" has avoided a charge of "Inappropriate behaviour" ? ![]()
I can't vouch for his behavour but his use of English is truly shocking :-)))
*behaviour* ;-)
Christopher_M posted:*behaviour* ;-)
Who is confusing who ? ![]()
Don Atkinson posted:Christopher_M posted:*behaviour* ;-)
Who is confusing who ?
Is the space before the '?' for the missing 'm'?
Pedant that.
mmmmmm...... I wondered who would spot that and how long it would take.........
Adam Meredith posted:Don Atkinson posted:Christopher_M posted:*behaviour* ;-)
Who is confusing who ?
Is the space before the '?' for the missing 'm'?
Pedant that.
I would have said “ idiosyncratic” if I thought I could spell “idiosyncratic” and was sure it was the right word to use ![]()
Don Atkinson posted:Now for something a little more challenging
Four Circles
Its (pretty) obvious that the maximum number of different sized circles (excluding infinitely large circles that have become straight lines!) that can be made to 'just touch' one another is four. (each and every circle just touches the other three).
In the attached diagram above, the three circles (Yellow), (Green) and (Blue) have radii of 1, 2 and 3 respectively.What are the radii of the two 'fourth' circles (shown in red in the diagram below), that can be made to just touch each of Yellow, Green and Blue. (note the two 'fourth' circles will not touch each other, ‘cos that would break the maximum rule!!)
Oh! BTW, there is a standard way and an elegant way to solve this little problem.
As I said above, No need to look back !! ![]()
OK.
1247 divided by 43 equals 29
The other missing numbers are 86 and 387.
sjbabbey posted:OK.
1247 divided by 43 equals 29
The other missing numbers are 86 and 387.
Nicely done SJB
That just leaves the Red Circles (for the moment) - anyone ? (Frank is excluded)
Don
I wouldn't like a nice problem to go to waste. So with a "little" help from Mr Google I went in pursuit of the elegant solution for the circles problem.
I get the following:
Radius of inscribed (inner) circle: 6/23
Radius of circumscribed circle (outer): 6
The alternative geometry-based solution looks pretty messy - and I soon ran out of patience !
Cheers,
Peter
sophiebear0_0 posted:Don
I wouldn't like a nice problem to go to waste. So with a "little" help from Mr GoogleI went in pursuit of the elegant solution for the circles problem.
I get the following:
Radius of inscribed (inner) circle: 6/23
Radius of circumscribed circle (outer): 6
The alternative geometry-based solution looks pretty messy - and I soon ran out of patience !
Cheers,
Peter
I hope you found the "elegant" solution interesting.
It's surprising what we all forget as we grow older and become more specialised in our work and hobbies.
Using 1/r to represent "Curvature" is something I find most people have forgotten about !
Don Atkinson posted:Using 1/r to represent "Curvature" is something I find most people have forgotten about !
Always assuming they knew it in the first place :-)
Christopher_M posted:Don Atkinson posted:Using 1/r to represent "Curvature" is something I find most people have forgotten about !Always assuming they knew it in the first place :-)
eeK !!!.......Chris, what sort of school did you go to ! .......(probably had to settle for Harrow rather than Eaton ?) but at least NOW you know ![]()
And the circles with radii 1, 2 and 3 work out in a very satisfying way when using what I think is a rather elegant formula. Keep everything in vulgar fractions (none of this modern decimalisation) and they virtually cancel themselves out. All very neat.
sophiebear0_0 posted:Don
I wouldn't like a nice problem to go to waste. So with a "little" help from Mr Google I went in pursuit of the elegant solution for the circles problem.
I get the following:
Radius of inscribed (inner) circle: 6/23
Radius of circumscribed circle (outer): 6
The alternative geometry-based solution looks pretty messy - and I soon ran out of patience !
Cheers,
Peter
Hi Peter,
There's nothing wrong with using the internet. Most of us would have to get a text book out to brush up on geometry if we tried it from scratch. Using the internet sensibly is just the same as reading a book !
A couple of easy ones again, before the next "hard one"
Dishing up the Prize Money
Nine people, Adam, Bruce, Chris, Dave, Erik, Frank, Graham, Huge and Ian, share a prize of £450.
Bruce gets £1 more than Adam. Chris gets £1 more than Bruce. Dave gets £1 more than Chris and so on.
How much of the £450 does Ian get ?