A Fistful of Brain Teasers

Now for something more down to earth....

TETHERED GOAT EATS GRASS.....

Near a small town with a big cathedral, a retired electronics worker named Paul, supplements his meagre pension with part-time farming. Paul rents a circular field of grass of 100m radius but he owns a very hungry goat from which he derives milk for cheese. Paul wishes to tie the goat to a post on the circumference of the field and wants to manage the growth of the grass so the goat doesn't decimate it too quickly. He therefore decides to use just enough rope so that the goat can only eat 50% of the grass.

What must the length of the rope be? Assume the distance between the jaws of the goat and the point of attachment of the rope is insignificant.

Now at the risk of upsetting Eloise, the answer on its own will attract an “OK” (you can probably look it up on the internet anyway). But a “Neat, well done” will only follow a bit of revealed calculation.

sjbabbey posted:

168 nautical miles from A i.e. 72 nautical miles short of B

168/150 = 1.12 hours

168/90 = 1.8777 hours

total =     2.9977 hours

Hi sj,

I'm guessing that you might have used a spreadsheet to "nudge" the distance further and further away from the departure point, until you found the point at which a return would not be possible.

I'm sure the airlines these days have sophisticated computer programs, especially for their long haul and trans-Atlantic flights, to figure out the probable wind speed at various altitudes and positions along their route. This, together with aircraft performance data,will help them figure out best power settings, requested altitudes and a host of other parameters to meet their schedules at minimal cost.

So if you did use the "spreadsheet nudge" process, you are in good company !

No spreadsheet. Simply trial and error using my PC's calculator.

sjbabbey posted:

No spreadsheet. Simply trial and error using my PC's calculator.

You did well. 

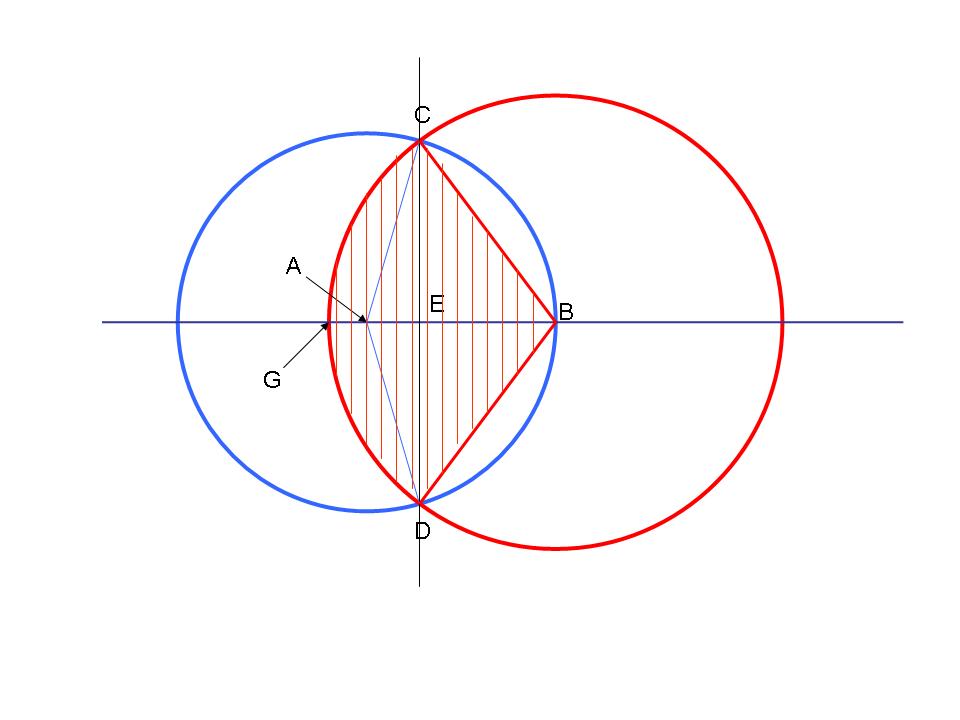
Back to the Goat & Grass......

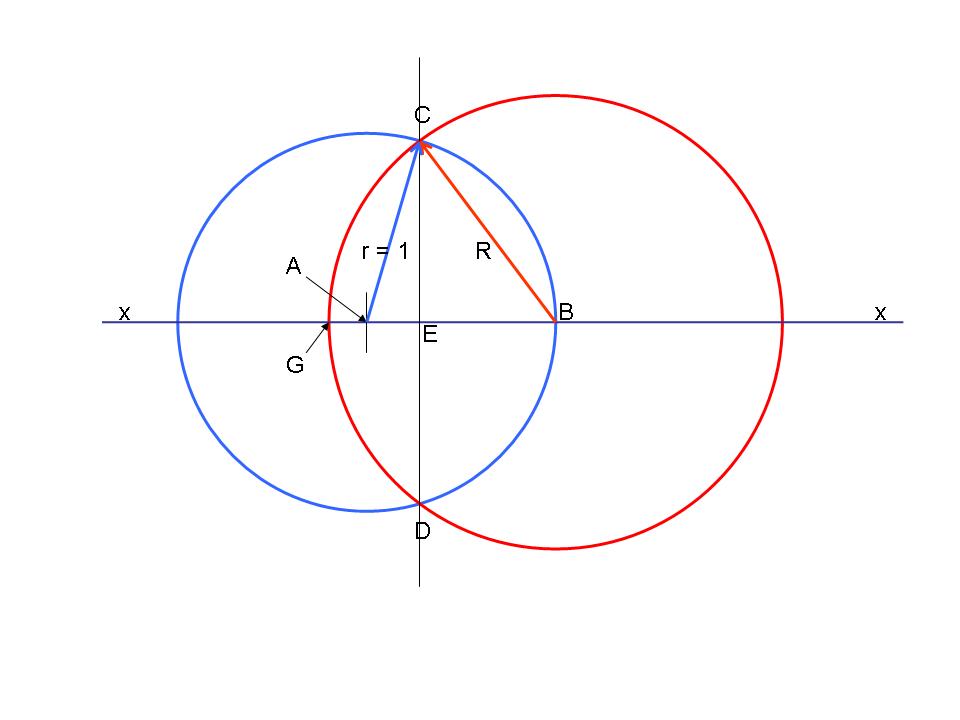
The Blue circle represents the field so AC = AD = 1     ok 100 m, but call it 1 and remember it's 100m !

The red circle represents the length of the rope which is fixed to a post on the circumference of the field, at point B. So BC = BD = R = Length of the rope. And the overlap of the two circles is π/2 ie half the area of a field radius 1 (but remember it's actually 100m)

All you need to do now is work out  a few lengths eg CE and a few areas of a triangle and a couple of circular segments (keeping everything in Radians) and ......................bingo......

............you have a formula..........(of sorts!)

Yes, this one is easy to understand but a bit more challenging to resolve !!!!!!!  it will certainly sort the sheep from the goats...

ISTR that in recent years Probability has been in the maths curriculum more so than Geometry. So leaving aside for the moment the probability of somebody solving the Goat/Grass problem without a bit of facilitation, I thought it possible you might like to energise the grey matter with a few examples involving probability !

Probability

Consider tossing three fair coins. What is the probability of them landing with two heads and one tail showing ?

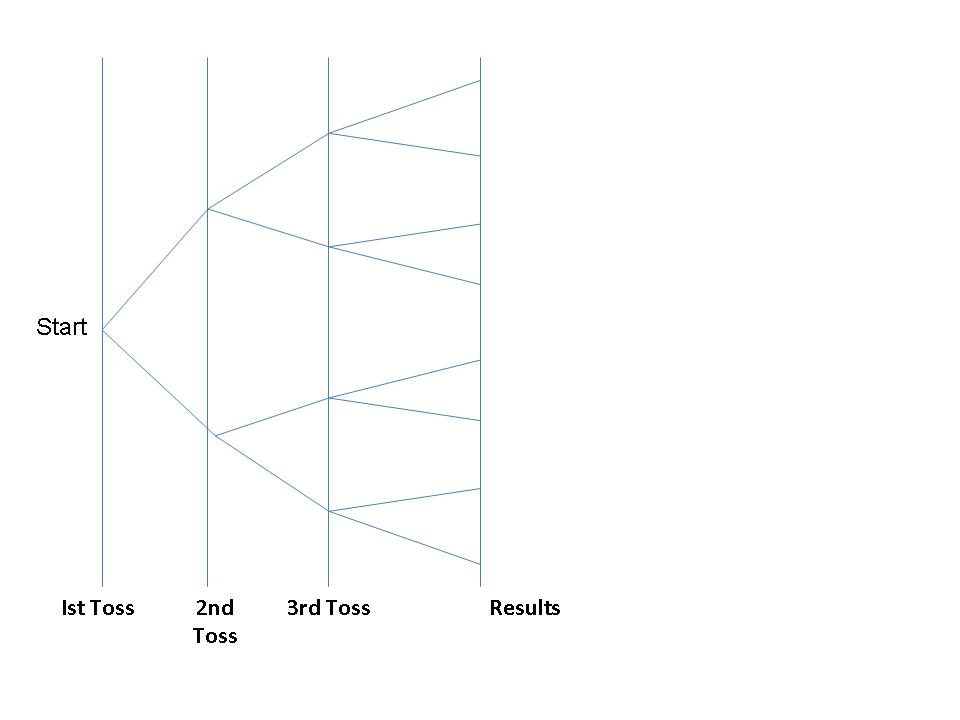
For many probability questions, I find it helps to start with a "tree" diagram like the one above.

When the outcome of an "Event" is 50/50, (as in the 3-coins), there is little point in adding the probability of each outcome. since all outcomes are equally likely.

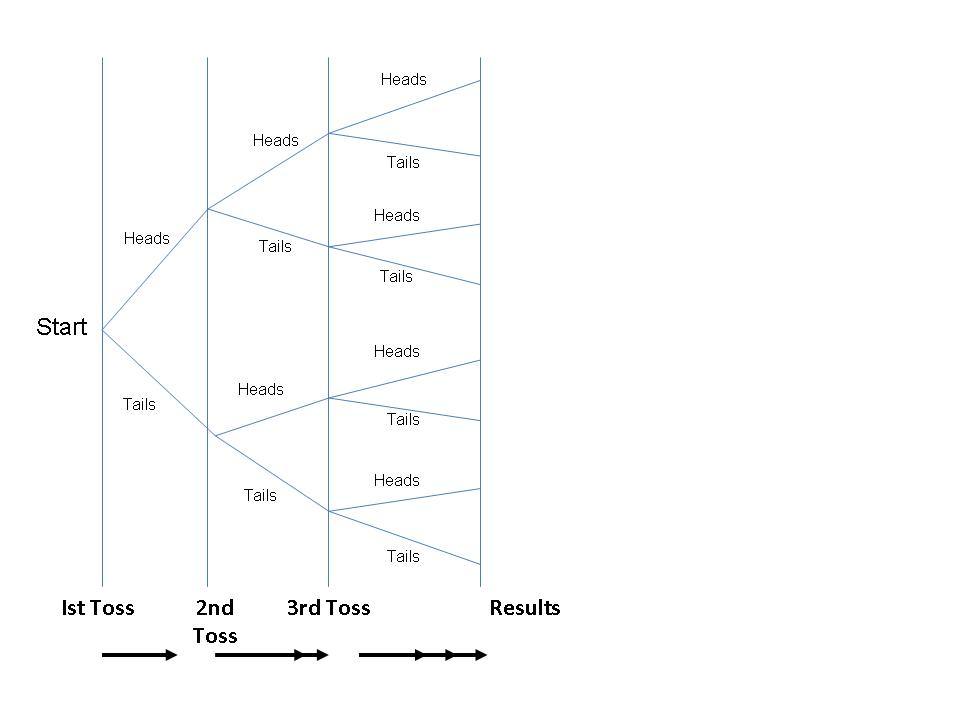
Eight possible outcomes.

Only some of which are HHT............(or THH.....or HTH.....) ie two Heads and one Tails

Step-by-step solution to the Tethered Goat teaser (it is just geometry)

More to follow, just one step at a time.

Please jump in with your solution - it might be quicker........

Associated text is below

So far it's straight forward, but apologies if I have incorporated any "typos"

Another couple of pictures to follow

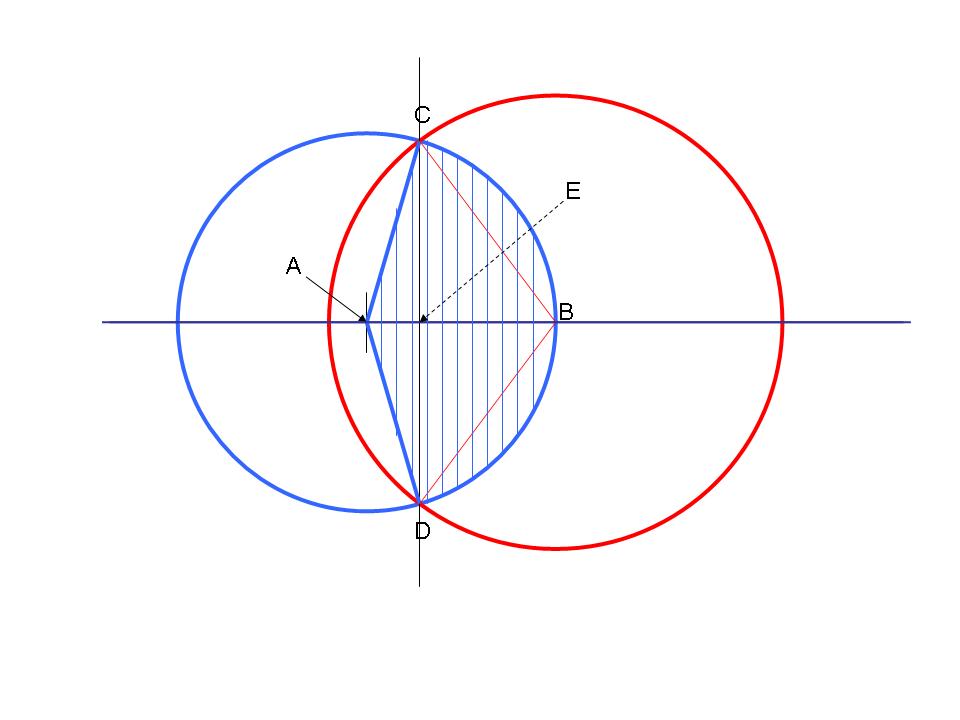
One more picture, then the maths.........

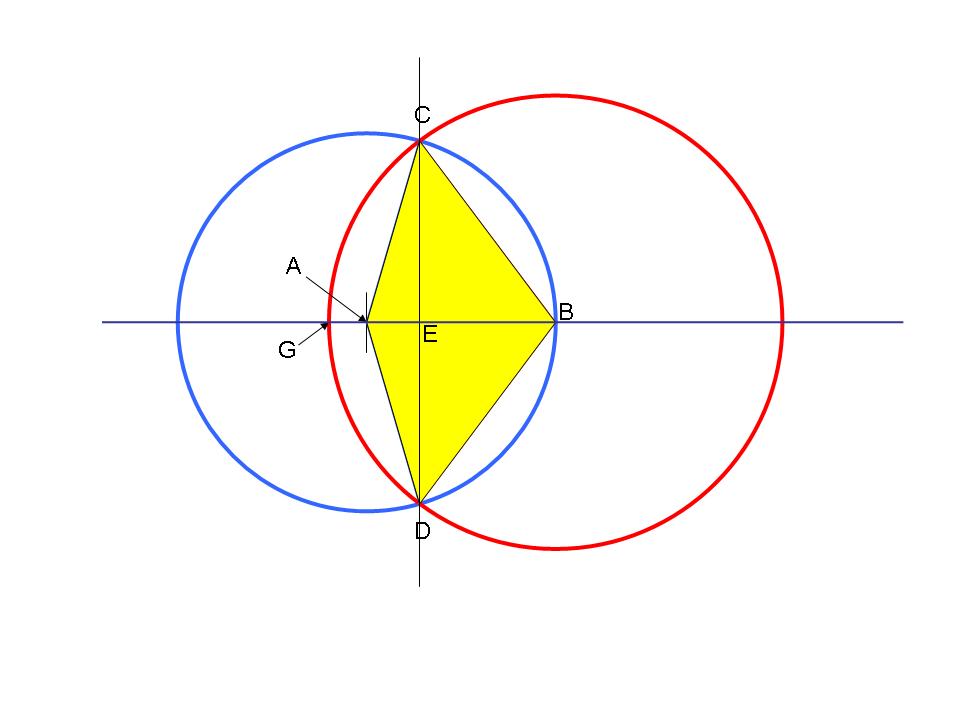
This picture is important !

I'll leave it here for a day or two, give you time to absorb or jump in.

I'm aware that very few people would need this reminder, it's just in here for the sake of completeness !

I'm sticking with Radians because :-

• it's easier to write down the equations
• the arithmetic will be done in Excel, and by default, Excel uses Radians !

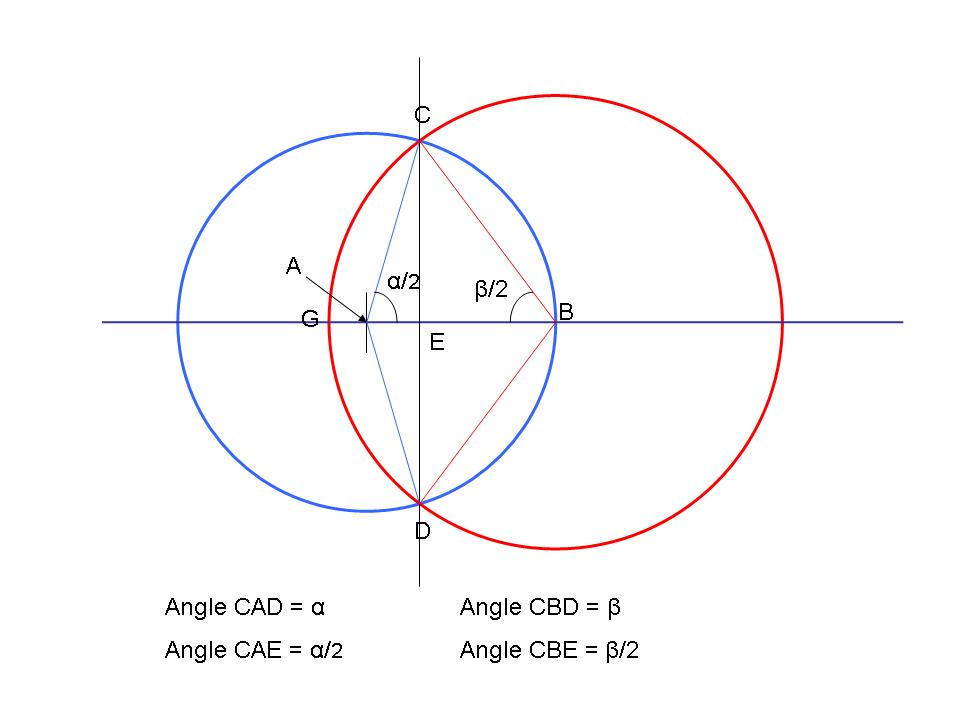
That funny symbol for Angle CAD = α is meant to be the Greek letter "Alpha"

There is more to follow (obviously) but you don't need to learn the Greek alphabet, you might like to, but you don't need  to.

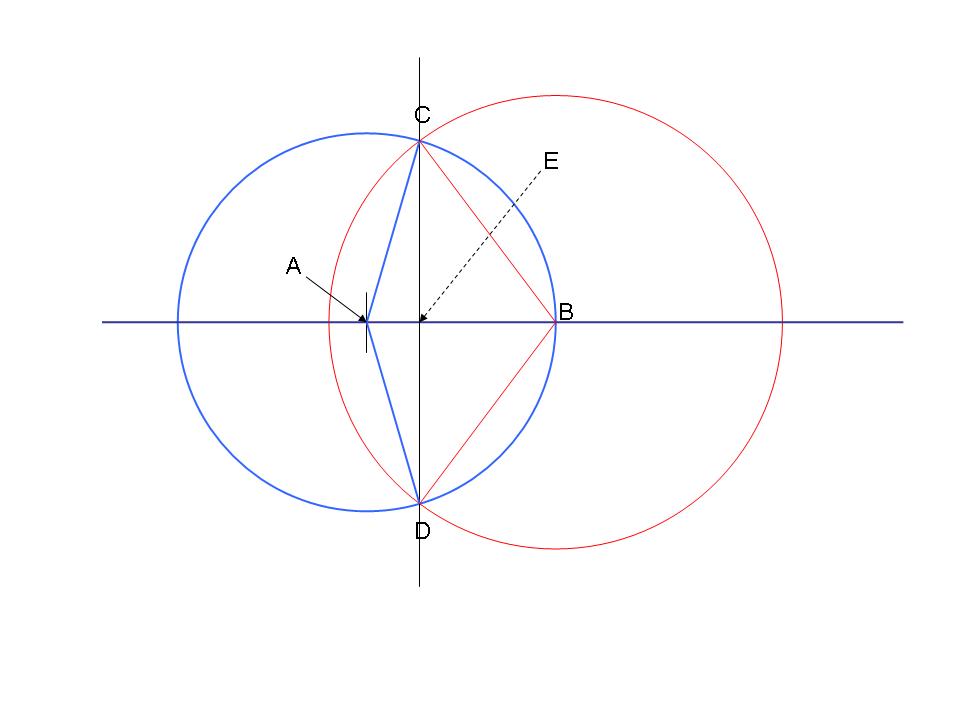
This is the beginning of the end, so to speak.

This post plus the following diagram and the post after that, just about nail it !

The yellow triangle is exactly half the "diamond" ACBD and AB = 1 (ie the radius of the field)

So the "height" CE is, in effect, the area of the "diamond"

BE and AE are needed to help figure out the size of those angles α and β, but that's about all the Greek you need to know

The "End of the End" will follow shortly.

The above picture just sumarises the essential elements of my solution and the final expression for R  (in yellow).

The next post outlines how I obtained a value for R using this expression - it's pig-ugly, but works

Can anybody find a unique numerical solution for R, rather than fumbling around with the above expression ?

Of course, you don't have to use Excel. You can do the iterations by hand, using Trig tables (assuming you kept them from your school-days)

I'll post a snap-shot of my solution (the above picture has given you a good start......) and Excel spread sheet later today or tomorrow.