Maths home work problem...!
Posted by: bob atherton on 07 February 2009
Here is a question that has been puzzling our son, my wife and me. The question is from a maths GCSE paper. This is meant to be answered by Harry, who is 14.
The force of attraction F between two magnets varies inversely as the square of the distance d between them.
When magnets are 1.5 cm apart, the force of attraction is 28 Newtons
(a) Find an equation connecting F and d.
(b) What is the distance between the magnets when the force of attraction in 43.75 Newtons?
Your help with Harry’s homework would be very much appreciated!
Thanks, Bob & Harry.
The force of attraction F between two magnets varies inversely as the square of the distance d between them.
When magnets are 1.5 cm apart, the force of attraction is 28 Newtons
(a) Find an equation connecting F and d.
(b) What is the distance between the magnets when the force of attraction in 43.75 Newtons?
Your help with Harry’s homework would be very much appreciated!
Thanks, Bob & Harry.
Posted on: 07 February 2009 by gone
I shall probably end up with egg all over my face, but I think the basic equation is F=X/(d^2) where X is a constant?
If so, then you can solve X as being 0.0063-ish (remember to use metres and not centimetres).
So if I'm right, (b) gives the answer 1.2cm?
Blimey, who said exams were getting easier.....?
If so, then you can solve X as being 0.0063-ish (remember to use metres and not centimetres).
So if I'm right, (b) gives the answer 1.2cm?
Blimey, who said exams were getting easier.....?
Posted on: 07 February 2009 by SigmundEinstein
F=63/(d*d)
If F=43.75N, then d=1.2cm
I think
If F=43.75N, then d=1.2cm
I think
Posted on: 07 February 2009 by 555
The Exceptional Brain of Sigmund Einstein
The gross anatomy of Einstein's brain was within normal limits with the exception of his parietal lobes. In each hemisphere, morphology of the Sylvian fissure was unique compared with 182 hemispheres from the 35 control male and 56 female brains: the posterior end of the Sylvian fissure has a relatively anterior position, associated with no parietal operculum. In this same region, Einstein's brain was 15% wider than controls. These two features suggest that, in Einstein's brain, extensive development of the posterior parietal lobes occurred early, in both longitudinal and breadth dimensions, thereby constraining the posterior expansion of the Sylvian fissure and the development of the parietal operculum, but resulting in a larger expanse of the inferior parietal lobe.
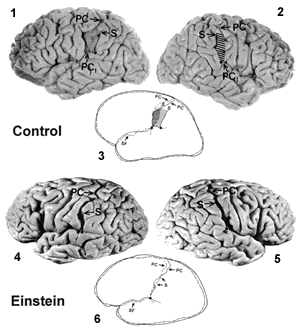
The photographs of the control brain show the parietal operculum in the left (stippled) and right (hatched) hemisphere, situated between the postcentral (PC) sulcus and the posterior ascending branch of the Sylvian fissure (SF), which originates at the point of bifurcation (•) and terminates at S. PC sub 1 is the inferior end of PC at SF. The tracing of the superimposed hemispheres (3) shows the asymmetry in position and size between the parietal opercula. The tracings of Einstein's hemispheres (6) highlights the confluence of PC and the posterior ascending branch of SF in each hemisphere, the absence of the parietal opercula, and the symmetry of the sulcal morphology between hemispheres. Comparison of the tracings shows the relatively anterior position of the SF bifurcation in Einstein, and the associated greater posterior parietal expanse, particularly in his left hemisphere compared with the control brain.
The gross anatomy of Einstein's brain was within normal limits with the exception of his parietal lobes. In each hemisphere, morphology of the Sylvian fissure was unique compared with 182 hemispheres from the 35 control male and 56 female brains: the posterior end of the Sylvian fissure has a relatively anterior position, associated with no parietal operculum. In this same region, Einstein's brain was 15% wider than controls. These two features suggest that, in Einstein's brain, extensive development of the posterior parietal lobes occurred early, in both longitudinal and breadth dimensions, thereby constraining the posterior expansion of the Sylvian fissure and the development of the parietal operculum, but resulting in a larger expanse of the inferior parietal lobe.

The photographs of the control brain show the parietal operculum in the left (stippled) and right (hatched) hemisphere, situated between the postcentral (PC) sulcus and the posterior ascending branch of the Sylvian fissure (SF), which originates at the point of bifurcation (•) and terminates at S. PC sub 1 is the inferior end of PC at SF. The tracing of the superimposed hemispheres (3) shows the asymmetry in position and size between the parietal opercula. The tracings of Einstein's hemispheres (6) highlights the confluence of PC and the posterior ascending branch of SF in each hemisphere, the absence of the parietal opercula, and the symmetry of the sulcal morphology between hemispheres. Comparison of the tracings shows the relatively anterior position of the SF bifurcation in Einstein, and the associated greater posterior parietal expanse, particularly in his left hemisphere compared with the control brain.
Posted on: 07 February 2009 by Happy Listener
Right answers but marks go to the way you get there nowadays!
So think like this -
If distance = 1.5cm and the strength is inversely proportional, then when there is no distance, strength will be 1.5 squared = 2.25x x 28 = 63 i.e the constant.
So, derived =: force = 63/distance squared
or better derived f x distance squared = 63
or distance squared = 63/force
so..solution = distance squared = 63/43.75 (=1.44).
Root of 1.44x = 1.2cm
So think like this -
If distance = 1.5cm and the strength is inversely proportional, then when there is no distance, strength will be 1.5 squared = 2.25x x 28 = 63 i.e the constant.
So, derived =: force = 63/distance squared
or better derived f x distance squared = 63
or distance squared = 63/force
so..solution = distance squared = 63/43.75 (=1.44).
Root of 1.44x = 1.2cm
Posted on: 07 February 2009 by u77033103172058601
Happy listener....????WTF?
If strength is inversely proportion to the distance squared, which is the given assumption then at zero distance the force is infinite! So you get no marks for your derivation.
The second answer was right
F = Constant/d*d
Irrespective of the units the value of the constant is then easily derived.
Alternatively
F1/F2 = d2*d2/d1*d1 using the usual notation.
From which the 1.2cm can be easily derived.
Quite honestly, this is a question which is far or should be far too easy for a 14 year old
If strength is inversely proportion to the distance squared, which is the given assumption then at zero distance the force is infinite! So you get no marks for your derivation.
The second answer was right
F = Constant/d*d
Irrespective of the units the value of the constant is then easily derived.
Alternatively
F1/F2 = d2*d2/d1*d1 using the usual notation.
From which the 1.2cm can be easily derived.
Quite honestly, this is a question which is far or should be far too easy for a 14 year old
Posted on: 07 February 2009 by winkyincanada
PD
Posted on: 08 February 2009 by bob atherton
Thank you to all of you for your kind help with Harry’s home work. I must confess that IMHO these questions were pretty tough for a 14 year old, let alone a 52 year old like me!
I have always found these type of maths questions intriguing puzzles and yet often a source of frustration with not being able to find the answer. I think we all have preferred ways of learning and for me it visual, hands on, every time.
If ever a problem in life involves magnetic attraction and working out of the forces I’m reasonably confident I will get it sorted.
Thanks again, Bob & Harry
I have always found these type of maths questions intriguing puzzles and yet often a source of frustration with not being able to find the answer. I think we all have preferred ways of learning and for me it visual, hands on, every time.
If ever a problem in life involves magnetic attraction and working out of the forces I’m reasonably confident I will get it sorted.
Thanks again, Bob & Harry
Posted on: 08 February 2009 by Musicmad
Bob, I read and smiled at your question and the responses last evening and recited them to my wife ... a maths' teacher (11-18yrs old) of nearly 30 years' standing. She took exception to the suggestion that this is an easy question for a "14 yr old" and this morning said it had bothered her and that I should reply.
She tells me that it is higher level (i.e. more able students) topic taught, most probably, in year 10 (14 - 15 yr olds).
As with most maths' topics - if not all topics across the educational spectrum - it's easy if you know how.
Mitch
She tells me that it is higher level (i.e. more able students) topic taught, most probably, in year 10 (14 - 15 yr olds).
As with most maths' topics - if not all topics across the educational spectrum - it's easy if you know how.
Mitch
Posted on: 08 February 2009 by SigmundEinstein
I agree with music mad. It's only alarming if you think everybody should be above average at everything.
Posted on: 08 February 2009 by Howlinhounddog
As someone who always loved Maths at school but for some reason had no ability in the subject an hour after leaving any Maths lesson I attended, congratulations one and all (including 14 y.o. Sibs and those who were incorrect).
After one reading of the problem I was taken back 30 odd years to that pimpily glazed over little boy in the Maths class I once was.
Did'nt understand a bloody bit of it
After one reading of the problem I was taken back 30 odd years to that pimpily glazed over little boy in the Maths class I once was.
Did'nt understand a bloody bit of it
Posted on: 09 February 2009 by rodwsmith
quote:Originally posted by SigmundEinstein:
I agree with music mad. It's only alarming if you think everybody should be above average at everything.
Some sage once said:
"Imagine someone of average intelligence. Now realise that half the people you meet are more stupid than that."
Which gives me comfort.
Whilst I fully understood the answers above, I have to say that the question flummoxed me a bit. I was good at maths at school, so I was mildly alarmed that it was considered routine for a 14 year old. Still I'm not sure I could solve a quadratic equation these days, or even that I'd recognise one immediately. And I don't think I ever knew what practical purpose they served.
But I'm much better with a corkscrew than I was back then...
Posted on: 09 February 2009 by Fraser Hadden
quote:Imagine someone of average intelligence. Now realise that half the people you meet are more stupid than that.
Actually this describes someone of median intelligence which will not be the same as average (a.k.a.mean) intelligence if the intelligence distribution is skewed - as it is.
I'll get me coat!
Fraser
Posted on: 11 February 2009 by Wolf2
I remember taking Algebra in summer school to pass my last year of it. UGH!
I got the teacher really mad when I asked "but why?"
I got the teacher really mad when I asked "but why?"
Posted on: 11 February 2009 by Huwge
quote:Originally posted by Musicmad:
Bob, I read and smiled at your question and the responses last evening and recited them to my wife ... a maths' teacher (11-18yrs old) of nearly 30 years' standing. She took exception to the suggestion that this is an easy question for a "14 yr old" and this morning said it had bothered her and that I should reply.
She tells me that it is higher level (i.e. more able students) topic taught, most probably, in year 10 (14 - 15 yr olds).
As with most maths' topics - if not all topics across the educational spectrum - it's easy if you know how.
Mitch
iirc at Common Entrance we had to prove Pythagoras Theorem, so this question seems to reflect a dumbing down of subjects given that I was 12 when I did my CE exams. Also, this is just an extension of simple proportions which were one of the first things I seem to remember learning after my parrot fashion times tables. On the basis of this, my Physics O'level would seem like rocket science today I guess.
If you compare the A levels of 30 years ago, especially sciences, it is shocking how standards have slipped or did we expect too much of the kids then?
