A Fistful of Brain Teasers
Posted by: Don Atkinson on 13 November 2017
A Fistful of Brain Teasers
For those who are either non-British, or under the age of 65………. The UK used to have a brilliant system of currency referred to as “Pounds, Shillings and Pence”. Simplified to £ ״ s ״ d. No! Don’t ask me why the “Pence” symbol is a “d”, just learn it and remember it !
A £ comprised 20 Shillings and a Shilling comprised 12 Pence. Thus a £ comprised 240 Pence. I reckon that both Microsoft and Apple would have difficulty with these numbers in their spreadsheets, more so if we included Guineas, Crowns, Half-Crowns and Florins. However, I digress..............
The purpose of the explanation is to assist with the first two or three teasers that follow. So just to ensure a reasonable comprehension has been grasped…. ….. if each of three children has £3 − 7s − 9d, then collectively they have £10 − 3s − 3d Got the idea ? Good ! Just try 5 children, two each with £4 − 15s − 8d and three each with £3 − 3s − 4d. How much do they have between them ? (this isn’t the first brain teaser, just the basic introduction with some “homework”, the Teasers follow)
Don Atkinson posted:Any body going to tackle Ian’s neat puzzle searching for Pi ?
To be fair any credit belongs to Archimedes !
Ian G. posted:Don Atkinson posted:Any body going to tackle Ian’s neat puzzle searching for Pi ?
To be fair any credit belongs to Archimedes !
He doesn’t seem to post on this forum these days....... ![]()
Don Atkinson posted:Ian G. posted:Don Atkinson posted:Any body going to tackle Ian’s neat puzzle searching for Pi ?
To be fair any credit belongs to Archimedes !
He doesn’t seem to post on this forum these days.......
I’m sure he’s still floating about somewhere.
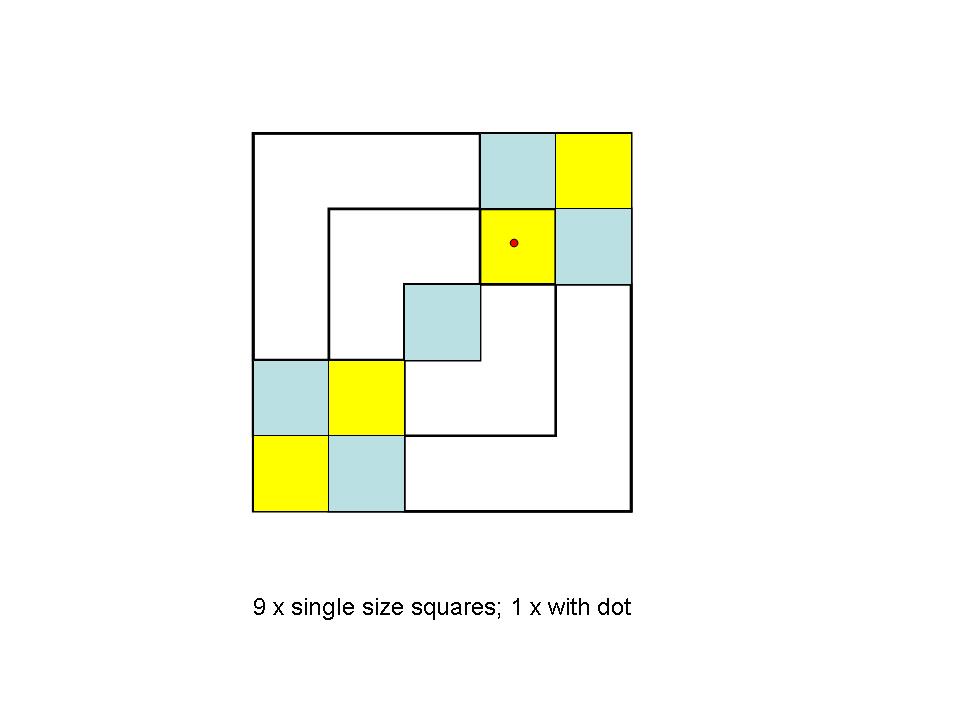
Eoink posted:Filipe posted:18, 5
best to count by size
Phil
Great tip, thanks Phil, I now get 18.
Well I can see 19 and 6...
Ian G. posted:Don Atkinson posted:Ian G. posted:Don Atkinson posted:Any body going to tackle Ian’s neat puzzle searching for Pi ?
To be fair any credit belongs to Archimedes !
He doesn’t seem to post on this forum these days.......
I’m sure he’s still floating about somewhere.
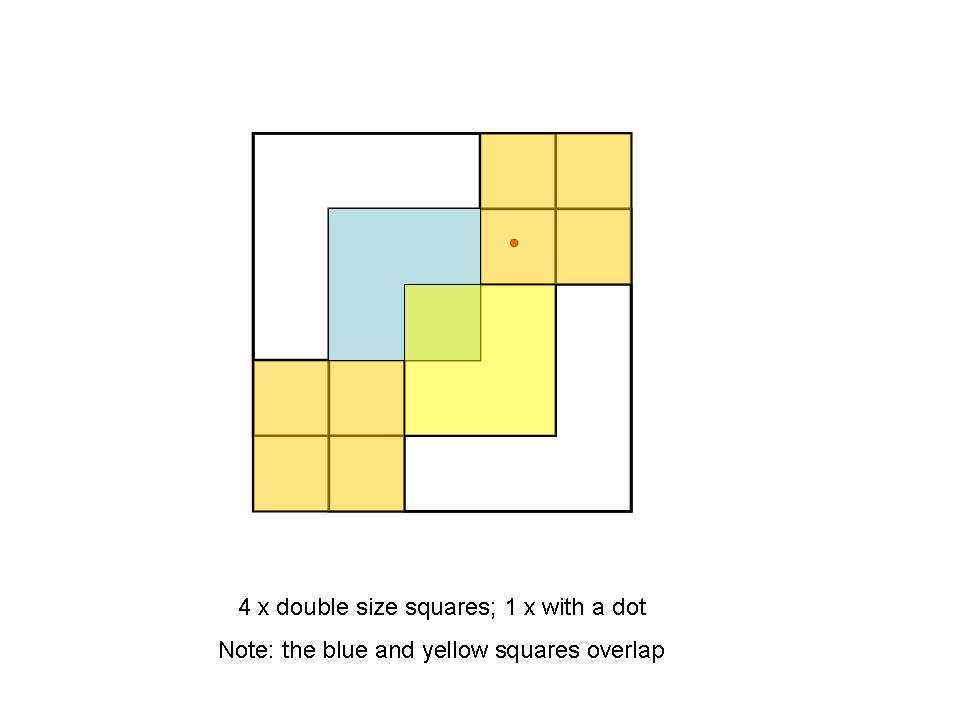
2.598 & 3.674
assuming I understood the question and assuming Pythagoras had done his bit before Archimedes. (Area of inner hex touching circle = 2.598r^2, outer is 3.674r^2)
having scribbled workings on phone screen I managed to delete when I went to copy for her, and this time of night not doing again, but this is part: area of inner hex calculates out to be
A=6x 0.866r x 0.5r
Innocent Bystander posted:Eoink posted:Filipe posted:18, 5
best to count by size
Phil
Great tip, thanks Phil, I now get 18.
Well I can see 19 and 6...
Interesting.
It's always great to find somebody with a different view point.
Now, i've looked and looked and can't see more than 18/5 ................... but......
................ I'm open to persausion and I guess the others are, especially Mike ?
Darn, I won’t be able to sleep now.
Stupid me, I missed one! It is 19 and 6 not 19 and 5.
I’m wrong twice, but. It three times. 19 & 6 is correct. Now I’m listening to music before bed and resting my cross eyes.
Innocent Bystander posted:Stupid me, I missed one! It is 19 and 6 not 19 and 5.
I posted that thinking I had said 19 and 5, but I see I had said 19 and 6 all along!
Innocent Bystander posted:Ian G. posted:Don Atkinson posted:Ian G. posted:Don Atkinson posted:Any body going to tackle Ian’s neat puzzle searching for Pi ?
To be fair any credit belongs to Archimedes !
He doesn’t seem to post on this forum these days.......
I’m sure he’s still floating about somewhere.
2.598 & 3.674
assuming I understood the question and assuming Pythagoras had done his bit before Archimedes. (Area of inner hex touching circle = 2.598r^2, outer is 3.674r^2)
having scribbled workings on phone screen I managed to delete when I went to copy for her, and this time of night not doing again, but this is part: area of inner hex calculates out to be
A=6x 0.866r x 0.5r
That works, but there is a better (tighter) pair of bounds you can get from same figures.
Ian G. posted:Innocent Bystander posted:Ian G. posted:Don Atkinson posted:Ian G. posted:Don Atkinson posted:Any body going to tackle Ian’s neat puzzle searching for Pi ?
To be fair any credit belongs to Archimedes !
He doesn’t seem to post on this forum these days.......
I’m sure he’s still floating about somewhere.
2.598 & 3.674
assuming I understood the question and assuming Pythagoras had done his bit before Archimedes. (Area of inner hex touching circle = 2.598r^2, outer is 3.674r^2)
having scribbled workings on phone screen I managed to delete when I went to copy for her, and this time of night not doing again, but this is part: area of inner hex calculates out to be
A=6x 0.866r x 0.5r
That works, but there is a better (tighter) pair of bounds you can get from same figures.
2*sqrt(3) > pi > 3
The inner equilateral triangles have chord of 1 (Unit circle). The outer is obtained with similar triangles and Pythagoras. Larger polygons give more accuracy.
Phil
Ian G. posted:Innocent Bystander posted:Ian G. posted:Don Atkinson posted:Ian G. posted:Don Atkinson posted:Any body going to tackle Ian’s neat puzzle searching for Pi ?
To be fair any credit belongs to Archimedes !
He doesn’t seem to post on this forum these days.......
I’m sure he’s still floating about somewhere.
2.598 & 3.674
assuming I understood the question and assuming Pythagoras had done his bit before Archimedes. (Area of inner hex touching circle = 2.598r^2, outer is 3.674r^2)
having scribbled workings on phone screen I managed to delete when I went to copy for her, and this time of night not doing again, but this is part: area of inner hex calculates out to be
A=6x 0.866r x 0.5r
That works, but there is a better (tighter) pair of bounds you can get from same figures.
I can see that with the inner one it should be simple to calculate construct 6 equilateral triangles with a side of the hexagon as base and apex on the circumference and calculate their areas as a function of the radius, to combine with the hex area - but that is going beyond the brief (You can find upper and lower bounds on the value of π geometrically using a circle and a couple of hexagons - one for the lower bound and one for the upper bound. What are the values of these two bounds on π ? ) I'm struggling to see how to get further with just 2 hexagons and a circle.
Adding those triangles outside the internal hexagon indeed calculates out as a total area of 3.0r^2 giving inner bound value for pi of 3 as Filipe calculated - but that in effect is using a dodecagon...
Innocent Bystander posted:Adding those triangles outside the internal hexagon indeed calculates out as a total area of 3.0r^2 giving inner bound value for pi of 3 as Filipe calculated - but that in effect is using a dodecagon...
Not really. I just drew the outer hexagon with the same spokes and moved the chord to become a tangent.
More accurate approximations can be made with the dodecahedron using the triangle sides already calculated.
Phil
Innocent Bystander posted:Adding those triangles outside the internal hexagon indeed calculates out as a total area of 3.0r^2 giving inner bound value for pi of 3 as Filipe calculated - but that in effect is using a dodecagon...
Filipe (whose answer is the correct one ) never mentioned anything about area, think about what the simplest definition of pi is.
Ian G. posted:Innocent Bystander posted:Adding those triangles outside the internal hexagon indeed calculates out as a total area of 3.0r^2 giving inner bound value for pi of 3 as Filipe calculated - but that in effect is using a dodecagon...
Filipe (whose answer is the correct one ) never mentioned anything about area, think about what the simplest definition of pi is.
Just to assist IB, think "perimeter of a circle" ie circumference = 2Πr
ISTR that way back in this thread or a previous teaser, I developed a formula for the perimeter of in inscribed or excribed polygon in which Pi tended towards 3.142 etc as n (the number of sides in the polygon) became large.
Innocent Bystander posted:Adding those triangles outside the internal hexagon indeed calculates out as a total area of 3.0r^2 giving inner bound value for pi of 3 as Filipe calculated - but that in effect is using a dodecagon...
IB,
Just think of the outer hexagon having sides of 2L and the perpendicular to where these sides are tangential to the circle (ie the radius) is R. Thus the right-angled triangles formed by each half, of each segment of the outer hexagon have sides L; 2L and R. There are 12 of these triangles, but they all form part of the basic hexagon.
The inner hexagon is more simply formed by six equalateral triangles each of side R.
Thus the perimeter of the hexagons are (Outer) (12.√3)R/4 and 6R
This leads to Phil's answer.
If you do as I suggested for the next approximation, the chord length comes out at
√(2 - √3) = Π/6
Π > 3.1058